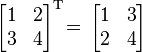转置矩阵- 算法、心得和多领域技术原理- gliethttp企业库|免费b2b网站

转置矩阵- 算法、心得和多领域技术原理- gliethttp

维基百科，自由的百科全书

在中，A 的转置是另一个矩阵A^T (也写做A^tr, ^tA 或A′)由下列等价动作建立:

把A 的横行写为A^T的纵列
把A 的纵列写为A^T的横行

形式上说，m × n 矩阵A 的转置是n × m 矩阵

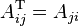$A^\mathrm{T}_{ij} = A_{ji}$ for $1 \le i \le n,$ $1 \le j \le m.$

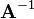注意 $\mathbf{A}^{T}$ （转置矩阵）与 $\mathbf{A}^{-1}$ （）不同。

$\begin{bmatrix} 1 & 2 \3 & 4 \end{bmatrix}^{\mathrm{T}} \!\! \;\! = \, \begin{bmatrix} 1 & 3 \2 & 4 \end{bmatrix}$

$\begin{bmatrix} 1 & 2 \3 & 4 \5 & 6 \end{bmatrix}^{\mathrm{T}} \!\! \;\! = \, \begin{bmatrix} 1 & 3 & 5\2 & 4 & 6 \end{bmatrix} \;$

对于矩阵A, B 和标量c 转置有下列性质:

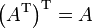
1. $\left( A^\mathrm{T} \right) ^\mathrm{T} = A \quad \,$

转置是自身。

2. $(A+B) ^\mathrm{T} = A^\mathrm{T} + B^\mathrm{T} \,$

转置是从m × n 矩阵的到所有n × m 矩阵的向量空间的。

3. $\left( A B \right) ^\mathrm{T} = B^\mathrm{T} A^\mathrm{T} \,$

注意因子反转的次序。以此可推出A 是，当且仅当A^T是可逆矩阵，在这种情况下有 (A⁻¹)^T = (A^T)⁻¹。相对容易的把这个结果扩展到矩阵相乘的一般情况，可得出 (ABC...XYZ)^T = Z^TY^TX^T...C^TB^TA^T。

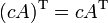
4. $(c A)^\mathrm{T} = c A^\mathrm{T} \,$

的转置是同样的标量。

5. $\det(A^\mathrm{T}) = \det(A) \,$

矩阵的转置矩阵的同于这个矩阵的行列式。

6.两个纵列向量a 和b 的可计算为

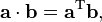
$\mathbf{a} \cdot \mathbf{b} = \mathbf{a}^{\mathrm{T}} \mathbf{b},$

7.如果A 只有元素，则A^TA 是。

8.如果A 是在某个上，则A 于A^T。

其转置等于自身的方块矩阵叫做；就是说A 是对称的，如果

$A^{\mathrm{T}} = A.\,$

其转置也是它的逆矩阵的方块矩阵叫做；就是说G 是正交的，如果

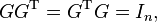$G G^\mathrm{T} = G^\mathrm{T} G = I_n , \,$ I是。

其转置等于它的负矩阵的方块矩阵叫做；就是A 是斜对称的，如果

$A^{\mathrm{T}} = -A.\,$

矩阵A 的，写为A^*，是A 的转置加上取每个元素的:

$A^* = (\overline{A})^{\mathrm{T}} = \overline{(A^{\mathrm{T}})}$

如果f: V→W 是在V和W之间的，我们定义f 的转置为线性映射^tf : W→V，确定自

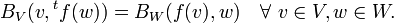
$B_V(v,{}^tf(w))=B_W(f(v),w) \quad \forall\ v \in V, w \in W.$

这里的，B_V和B_W分别是在V 和W 上的双线性形式。一个映射的转置的矩阵是转置矩阵，只要是关于它们的双线性形式是正交的。

在复向量空间上，经常用到来替代双线性形式。在这种空间之间的映射的转置可类似的定义，转置映射的矩阵由共轭转置矩阵给出，如果基是正交的。在这种情况下，转置也叫做。

如果V 和W 没有双线性形式，则线性映射f: V→W 的转置只能定义为在W 和V 之间的线性映射 ^tf : W^*→V^*。

郑重声明：资讯【转置矩阵- 算法、心得和多领域技术原理- gliethttp】由发布，版权归原作者及其所在单位，其原创性以及文中陈述文字和内容未经(企业库qiyeku.com)证实，请读者仅作参考，并请自行核实相关内容。若本文有侵犯到您的版权，请你提供相关证明及申请并与我们联系（qiyeku # qq.com）或【在线投诉】，我们审核后将会尽快处理。

—— 相关资讯 ——