介绍矩阵的编程表示,矩阵的初等变换,化阶梯矩阵及求方阵的行列式。
矩阵就是一个M×N平面的表格,用一个两维数组就可以表示,为了输入方便,我们用一个特殊格式的字符串对矩阵进行初始化,用"|"分割每一行,用","分割每一列,并增加一个Show的方法打印出矩阵,为了测试及调试的需要,还重写了ToString()方法。 代码
代码public class Matrix {
public int M { get; private set; }
public int N { get; private set; }
private readonly double[,] num = null;
#region 构造函数/Show
public Matrix(int m, int n, string input) {
M = m;
N = n;
num = new double[m, n];
if (!string.IsNullOrEmpty(input))
parseInput(input);
}
private void parseInput(string input) {
string[] rows = input.Split(new[] { '|' });
if (rows.Length != M)
throw new ArgumentException("row count err");
for (int i = 0; i < M; i++) {
string row = rows[i];
string[] cells = row.Split(new[] { ',' });
if (cells.Length != N)
throw new ArgumentException(string.Format("cells counte err:{0}", row));
for (int j = 0; j < N; j++) {
int cellValue;
if (!int.TryParse(cells[j], out cellValue))
throw new ArgumentException(string.Format("cell error:{0}", cells[j]));
num[i, j] = cellValue;
}
}
}
public void Show() {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++)
Console.Write("{0}\t", num[i, j]);
Console.WriteLine();
}
}
public override string ToString() {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
sb.Append(num[i, j]);
if (j != N - 1)
sb.Append(',');
}
if (i != M - 1)
sb.Append('|');
}
return sb.ToString();
}
}
public int M { get; private set; }
public int N { get; private set; }
private readonly double[,] num = null;
#region 构造函数/Show
public Matrix(int m, int n, string input) {
M = m;
N = n;
num = new double[m, n];
if (!string.IsNullOrEmpty(input))
parseInput(input);
}
private void parseInput(string input) {
string[] rows = input.Split(new[] { '|' });
if (rows.Length != M)
throw new ArgumentException("row count err");
for (int i = 0; i < M; i++) {
string row = rows[i];
string[] cells = row.Split(new[] { ',' });
if (cells.Length != N)
throw new ArgumentException(string.Format("cells counte err:{0}", row));
for (int j = 0; j < N; j++) {
int cellValue;
if (!int.TryParse(cells[j], out cellValue))
throw new ArgumentException(string.Format("cell error:{0}", cells[j]));
num[i, j] = cellValue;
}
}
}
public void Show() {
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++)
Console.Write("{0}\t", num[i, j]);
Console.WriteLine();
}
}
public override string ToString() {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
sb.Append(num[i, j]);
if (j != N - 1)
sb.Append(',');
}
if (i != M - 1)
sb.Append('|');
}
return sb.ToString();
}
}
先对这些代码进行单元测试,为了让代码块覆盖率达到{bfb},对构造函数的测试要故意模拟错误的输入,以便覆盖抛出异常的语句。
 代码
代码[TestMethod()]
public void MatrixConstructorTest() {
Matrix m;
try
{
m = new Matrix(2,2,"1,2|3,4|5,6");
Assert.Fail();
}
catch{}
try {
m = new Matrix(2, 2, "1,2|3,4,5");
Assert.Fail();
}
catch { }
try {
m = new Matrix(2, 2, "1,2|3,a");
Assert.Fail();
}
catch { }
}
[TestMethod]
public void toStringTest()
{
Matrix matrix = new Matrix(3, 3, "1,2,3|4,5,6|7,8,9");
Assert.IsTrue(matrix.ToString() == "1,2,3|4,5,6|7,8,9");
}
[TestMethod()]
public void ShowTest() {
Matrix matrix = new Matrix(2, 2, "1,2|3,4");
matrix.Show();
//这玩意还真没法儿测,不出错就算成功
}
public void MatrixConstructorTest() {
Matrix m;
try
{
m = new Matrix(2,2,"1,2|3,4|5,6");
Assert.Fail();
}
catch{}
try {
m = new Matrix(2, 2, "1,2|3,4,5");
Assert.Fail();
}
catch { }
try {
m = new Matrix(2, 2, "1,2|3,a");
Assert.Fail();
}
catch { }
}
[TestMethod]
public void toStringTest()
{
Matrix matrix = new Matrix(3, 3, "1,2,3|4,5,6|7,8,9");
Assert.IsTrue(matrix.ToString() == "1,2,3|4,5,6|7,8,9");
}
[TestMethod()]
public void ShowTest() {
Matrix matrix = new Matrix(2, 2, "1,2|3,4");
matrix.Show();
//这玩意还真没法儿测,不出错就算成功
}
矩阵的初等行变换虽然是很简单的变换,但用处非常大,包括行交换(两行交换位置),行倍乘(给某行乘以一个非零常数),行倍(某行乘以一个非零常数加到另一行上)加三种变换,因为行倍乘在求阶梯矩阵时用不到,就不写了。
 代码
代码//r1→r2,r2→r1
public void swapRow(int r1, int r2) {
double[] temp = new double[N];
for (int i = 0; i < N; i++)
temp[i] = num[r1, i];
for (int i = 0; i < N; i++)
num[r1, i] = num[r2, i];
for (int i = 0; i < N; i++)
num[r2, i] = temp[i];
}
//c×r1+r2
public void double_add(int r1, int r2, double c) {
for (int i = 0; i < N; i++) {
num[r2, i] += num[r1, i] * c;
}
}
public void swapRow(int r1, int r2) {
double[] temp = new double[N];
for (int i = 0; i < N; i++)
temp[i] = num[r1, i];
for (int i = 0; i < N; i++)
num[r1, i] = num[r2, i];
for (int i = 0; i < N; i++)
num[r2, i] = temp[i];
}
//c×r1+r2
public void double_add(int r1, int r2, double c) {
for (int i = 0; i < N; i++) {
num[r2, i] += num[r1, i] * c;
}
}
 代码
代码[TestMethod()]
public void swapRowTest() {
Matrix matrix = new Matrix(2,2,"1,2|3,4");
matrix.swapRow(0, 1);
Assert.IsTrue(matrix.ToString() == "3,4|1,2");
}
[TestMethod()]
public void double_addTest() {
Matrix matrix = new Matrix(2,2,"1,2|3,4");
matrix.double_add(0,1,2);
Assert.IsTrue(matrix.ToString() == "1,2|5,8");
}
public void swapRowTest() {
Matrix matrix = new Matrix(2,2,"1,2|3,4");
matrix.swapRow(0, 1);
Assert.IsTrue(matrix.ToString() == "3,4|1,2");
}
[TestMethod()]
public void double_addTest() {
Matrix matrix = new Matrix(2,2,"1,2|3,4");
matrix.double_add(0,1,2);
Assert.IsTrue(matrix.ToString() == "1,2|5,8");
}
阶梯矩阵在矩阵算法中有很重要的作用,比如在解线性方程时,先化为阶梯阵,再从未知数最少的方程逐步回代求解,或者求矩阵的秩的时候先化成阶梯矩阵,再去数非零的行数。
任何一个矩阵都可以转换成阶梯矩阵,方法是一列一列去转换。
注:A表示矩阵,_标识下标,{dy}个下标表示行,第二个下标表示列
1、从A_1_1开始,假设A_1_1非0(如果为0,则和其他首非零行交换),把A_1_1记做a
2、如果A_2_1为非0,记做b,那么{dy}行乘以-(b/a)加到第二行上,这时第二行首为零。
3、依次类推,把从A_2_1,A_3_1,...,A_m_1都化为0.
4、转向A_2_2,假设假设A_2_2非0(如果为0,则和其他第二列非零行交换),把A_2_2记做a
5、如果A_3_2为非0,记做b,那么{dy}行乘以-(b/a)加到第三行上,这时第三行第二为零。
6、依次类推,把从A_3_2,A_4_2,...,A_m_2都化为0.
7、依次类推,没重复一次1-3步的操作,都会把一列的指定行下面均化为0,最终可得到阶梯矩阵。
 代码
代码public void toStrassen() {
int start_row = 0, start_col = 0;
for (int col = 0; col < N; col++) {//一列一列去处理
var no_zero_col = get_no_zero_col(start_row, start_col);
if (no_zero_col == -1) return; //从该行该列向下向右全为0,直接返回
make_col_zero(no_zero_col, start_row);
start_row++;
if (no_zero_col == N - 1)
return;
start_col = ++no_zero_col;
}
}
//通过倍加运算使某一列从某个起始行开始下面的数为0
private void make_col_zero(int col, int start_row) {
for (int row = start_row + 1; row < M; row++) {
var z = num[row, col] / num[start_row, col];
double_add(start_row, row, -z);
}
}
// 获取从指定起始行和起始列开始的非零列。
//如果在起始列上从起始行开始找到非零行,但不是给定起始行,那么利用初等变化交换这两行。
// 如果在起始列上未找到非零行,那么起始行不变,起始列右移重新计算
private int get_no_zero_col(int start_row, int start_col) {
for (int row = start_row; row < M; row++) {
if (num[row, start_col] == 0) continue;
swapRow(row, start_row);
return start_col;
}
for (int col = start_col + 1; col < N; col++) {
for (int row = start_row; row < M; row++) {
if (num[row, col] == 0) continue;
swapRow(start_row, row);
return col;
}
}
return -1;
}
int start_row = 0, start_col = 0;
for (int col = 0; col < N; col++) {//一列一列去处理
var no_zero_col = get_no_zero_col(start_row, start_col);
if (no_zero_col == -1) return; //从该行该列向下向右全为0,直接返回
make_col_zero(no_zero_col, start_row);
start_row++;
if (no_zero_col == N - 1)
return;
start_col = ++no_zero_col;
}
}
//通过倍加运算使某一列从某个起始行开始下面的数为0
private void make_col_zero(int col, int start_row) {
for (int row = start_row + 1; row < M; row++) {
var z = num[row, col] / num[start_row, col];
double_add(start_row, row, -z);
}
}
// 获取从指定起始行和起始列开始的非零列。
//如果在起始列上从起始行开始找到非零行,但不是给定起始行,那么利用初等变化交换这两行。
// 如果在起始列上未找到非零行,那么起始行不变,起始列右移重新计算
private int get_no_zero_col(int start_row, int start_col) {
for (int row = start_row; row < M; row++) {
if (num[row, start_col] == 0) continue;
swapRow(row, start_row);
return start_col;
}
for (int col = start_col + 1; col < N; col++) {
for (int row = start_row; row < M; row++) {
if (num[row, col] == 0) continue;
swapRow(start_row, row);
return col;
}
}
return -1;
}
 代码
代码[TestMethod()]
public void toStrassenTest() {
Matrix matrix = new Matrix(4, 4, "0,1,-1,1|2,-2,1,1|2,3,-5,7|2,16,-14,24");
matrix.toStrassen();
Assert.IsTrue(matrix.ToString() == "2,-2,1,1|0,1,-1,1|0,0,-1,1|0,0,0,8");
matrix = new Matrix(3, 5, "0,0,0,5,6|1,2,3,4,5|0,0,0,10,8");
matrix.toStrassen();
Assert.IsTrue(matrix.ToString() == "1,2,3,4,5|0,0,0,5,6|0,0,0,0,-4");
matrix = new Matrix(3, 3, "1,2,3|4,0,0|0,0,0");
matrix.toStrassen();
Assert.IsTrue(matrix.ToString() == "1,2,3|0,-8,-12|0,0,0");
}
public void toStrassenTest() {
Matrix matrix = new Matrix(4, 4, "0,1,-1,1|2,-2,1,1|2,3,-5,7|2,16,-14,24");
matrix.toStrassen();
Assert.IsTrue(matrix.ToString() == "2,-2,1,1|0,1,-1,1|0,0,-1,1|0,0,0,8");
matrix = new Matrix(3, 5, "0,0,0,5,6|1,2,3,4,5|0,0,0,10,8");
matrix.toStrassen();
Assert.IsTrue(matrix.ToString() == "1,2,3,4,5|0,0,0,5,6|0,0,0,0,-4");
matrix = new Matrix(3, 3, "1,2,3|4,0,0|0,0,0");
matrix.toStrassen();
Assert.IsTrue(matrix.ToString() == "1,2,3|0,-8,-12|0,0,0");
}
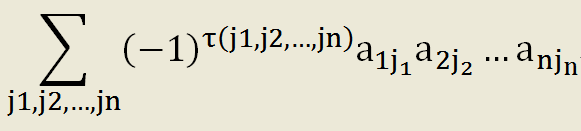
其中a是n阶方阵对应的行列式,τ表示对一个数列求逆序数,j1,j2,...jn是列下标,大概意思是行下标不变,是1,2,3,...,n,列下标是一个1,2,3,...,n的一个全排列(N级排列),然后每个多项式是n个分量相乘,这个分量的行下标是1-n顺序排列,列下标是n级排列的其中一个。
这里用到了N级排列,所以先写个辅助类来求N级排列
 代码
代码//计算一个N级排列
public static IEnumerable<int[]> permute(int n) {
if (n < 0) throw new ArgumentException();
List<int[]> ret = new List<int[]>();
int[] used = new int[n];
int[] p = new int[n];
int[] data = new int[n];
for (int i = 0; i < n; i++)
data[i] = i;
permute(ret, n, 0, used, p, data);
return ret;
}
//从一个数的集合里选注N个数的排列组合,使用回溯算法,复杂度应该是O(n!)
//http://blog.chinaunix.net/u/10638/showart.php?id=52814
private static void permute(ICollection<int[]> list, int n, int pos, int[] used, int[] p, int[] data) {
if (pos == n) {
int[] temp = new int[n];
p.CopyTo(temp, 0);
list.Add(temp);
return;
}
for (int i = 0; i < n; i++) {
if (used[i] != 0) continue;
used[i]++;
p[pos] = data[i];
permute(list, n, pos + 1, used, p, data);
used[i]--;
}
}
public static IEnumerable<int[]> permute(int n) {
if (n < 0) throw new ArgumentException();
List<int[]> ret = new List<int[]>();
int[] used = new int[n];
int[] p = new int[n];
int[] data = new int[n];
for (int i = 0; i < n; i++)
data[i] = i;
permute(ret, n, 0, used, p, data);
return ret;
}
//从一个数的集合里选注N个数的排列组合,使用回溯算法,复杂度应该是O(n!)
//http://blog.chinaunix.net/u/10638/showart.php?id=52814
private static void permute(ICollection<int[]> list, int n, int pos, int[] used, int[] p, int[] data) {
if (pos == n) {
int[] temp = new int[n];
p.CopyTo(temp, 0);
list.Add(temp);
return;
}
for (int i = 0; i < n; i++) {
if (used[i] != 0) continue;
used[i]++;
p[pos] = data[i];
permute(list, n, pos + 1, used, p, data);
used[i]--;
}
}
 代码
代码[TestMethod()]
public void permuteTest() {
try
{
MathHelper.permute(-1);
}
catch (Exception ex)
{
Assert.IsInstanceOfType(ex, typeof(ArgumentException));
}
const int n = 3;
IEnumerable<int[]> actual = MathHelper.permute(n);
int len = 0;
List<string> expected = new List<string>() { "012", "021", "102", "120", "201", "210" };
List<string> actualstrs = new List<string>();
foreach (int[] ints in actual) {
string temp = string.Empty;
for (int i = 0; i < ints.Length; i++)
temp += ints[i].ToString();
actualstrs.Add(temp);
len++;
}
Assert.IsTrue(len == 6);
foreach (string s in expected)
Assert.IsTrue(actualstrs.Contains(s));
}
public void permuteTest() {
try
{
MathHelper.permute(-1);
}
catch (Exception ex)
{
Assert.IsInstanceOfType(ex, typeof(ArgumentException));
}
const int n = 3;
IEnumerable<int[]> actual = MathHelper.permute(n);
int len = 0;
List<string> expected = new List<string>() { "012", "021", "102", "120", "201", "210" };
List<string> actualstrs = new List<string>();
foreach (int[] ints in actual) {
string temp = string.Empty;
for (int i = 0; i < ints.Length; i++)
temp += ints[i].ToString();
actualstrs.Add(temp);
len++;
}
Assert.IsTrue(len == 6);
foreach (string s in expected)
Assert.IsTrue(actualstrs.Contains(s));
}
 代码
代码//计算一个排列中的逆序数,O(n^2)复杂度,没做优化
public static int ReverseNumber(int[] cols) {
if (cols == null) throw new ArgumentNullException();
int ret = 0;
int len = cols.Length;
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++)
if (cols[i] > cols[j])
ret++;
}
return ret;
}
public static int ReverseNumber(int[] cols) {
if (cols == null) throw new ArgumentNullException();
int ret = 0;
int len = cols.Length;
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++)
if (cols[i] > cols[j])
ret++;
}
return ret;
}
2, 4, 3, 1, 5这个排列中,2后面有1,4后面有3和1,3后面有1,共4个逆序,用例做单元测试的数据。
 代码
代码[TestMethod()]
public void ReverseNumberTest() {
try {
MathHelper.ReverseNumber(null);
}
catch (Exception ex) {
Assert.IsInstanceOfType(ex, typeof(ArgumentNullException));
}
int[] cols = new[] { 2, 4, 3, 1, 5 };
const int expected = 4;
int actual = MathHelper.ReverseNumber(cols);
Assert.AreEqual(expected, actual);
}
public void ReverseNumberTest() {
try {
MathHelper.ReverseNumber(null);
}
catch (Exception ex) {
Assert.IsInstanceOfType(ex, typeof(ArgumentNullException));
}
int[] cols = new[] { 2, 4, 3, 1, 5 };
const int expected = 4;
int actual = MathHelper.ReverseNumber(cols);
Assert.AreEqual(expected, actual);
}
有了两个辅助方法,就是用代码把公式写出来就行了
 代码
代码//∑_(j1,j2,…,jn)?〖(-1)^τ(j1,j2,…,jn) a_(1j_1 ) a_(2j_2 ) 〗…a_(nj_n )
public double detA() {
if (M != N)
throw new NotSupportedException();
double sum = 0.0D;
var permute = MathHelper.permute(M);
foreach (int[] cols in permute) {
int reverse_number = MathHelper.ReverseNumber(cols);
double temp = 1.0D;
for (int i = 0; i < M; i++) {
int j = cols[i];
temp *= num[i, j];
}
if (reverse_number % 2 == 0)
sum += temp;
else
sum -= temp;
}
return sum;
}
public double detA() {
if (M != N)
throw new NotSupportedException();
double sum = 0.0D;
var permute = MathHelper.permute(M);
foreach (int[] cols in permute) {
int reverse_number = MathHelper.ReverseNumber(cols);
double temp = 1.0D;
for (int i = 0; i < M; i++) {
int j = cols[i];
temp *= num[i, j];
}
if (reverse_number % 2 == 0)
sum += temp;
else
sum -= temp;
}
return sum;
}
 代码
代码[TestMethod()]
public void detATest() {
const int m = 4;
const int n = 4;
const string input = "4,-5,10,3|1,-1,3,1|2,-4,5,2|-3,2,-7,-1";
Matrix target = new Matrix(m, n, input);
const double expected = 1D;
double actual = target.detA();
Assert.AreEqual(expected, actual);
Matrix matrix = new Matrix(3, 2, "1,2|3,4|5,6");
try
{
matrix.detA();
Assert.Fail();
}
catch{}
}
public void detATest() {
const int m = 4;
const int n = 4;
const string input = "4,-5,10,3|1,-1,3,1|2,-4,5,2|-3,2,-7,-1";
Matrix target = new Matrix(m, n, input);
const double expected = 1D;
double actual = target.detA();
Assert.AreEqual(expected, actual);
Matrix matrix = new Matrix(3, 2, "1,2|3,4|5,6");
try
{
matrix.detA();
Assert.Fail();
}
catch{}
}
这里演示了写一个简单的类库,并用单元测试来保证其质量的过程,矩阵还涉及到其它算法,数乘,乘法,求逆,求特征值,特征向量等,慢慢再实现。
其中求特征值是一个解一元N次方程的问题,xx用二分法弄了好几个小时也没弄出来,这里求一下代码,呵呵。-
竟然没有人来围观,我先坐个沙发
-
我来围观,可惜看不懂……
-
哪个show是可以测试的,既然是类库就不应该有Console这样的依赖,直接返回一个string,在调用的地方Console.Write就能测了
-
另外,没有必要因为追求{bfb}覆盖就写一些测试来凑数。测试覆盖率再高也只能代表你的测试覆盖了很多代码,无法代表所有路径都测到了,也没有办法代表质量没问题,覆盖率只是一个参考值,差不多就行了。
-
Nick Wang (懒人王)
恩,多谢指点,我还说那个Show不知道咋测试呢,呵呵,对于void的方法,并且不修改全局变量的方法是不是就不用测呀。
{bfb}的代码块儿覆盖率确实不能覆盖所有代码路径,这个我也发现了,呵呵,尽量提高就是了,一些防御性的代码我觉得也不需要做单元测试,想当然就会抛异常,用眼就能看出来。
郑重声明:资讯 【蛙蛙推荐:矩阵算法入门- 蛙蛙池塘- 博客园】由 发布,版权归原作者及其所在单位,其原创性以及文中陈述文字和内容未经(企业库qiyeku.com)证实,请读者仅作参考,并请自行核实相关内容。若本文有侵犯到您的版权, 请你提供相关证明及申请并与我们联系(qiyeku # qq.com)或【在线投诉】,我们审核后将会尽快处理。
—— 相关资讯 ——

