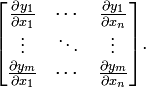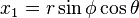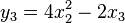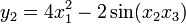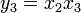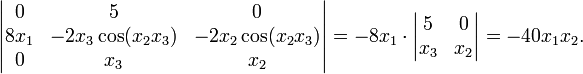雅可比矩阵

在中，雅可比矩阵是一阶以一定方式排列成的矩阵，其称为雅可比行列式。

还有，在中，的雅可比量表示：伴随该曲线的一个，曲线可以嵌入其中。

它们全部都以命名；英文雅可比量"Jacobian"可以发音为[ja ?ko bi ?n]或者[?? ?ko bi ?n]。

雅可比矩阵

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的{zy}线性逼近。因此，雅可比矩阵类似于多元函数的导数。

假设F:Rn→Rm 是一个从欧式n维空间转换到欧式m维空间的函数。这个函数由m个实函数组成: y1(x1,...,xn), ..., ym(x1,...,xn). 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵，这就是所谓的雅可比矩阵：

此矩阵表示为：

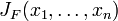，或者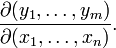

这个矩阵的第i行是由梯度函数的i(i=1,...,m)表示的

如果p是Rn中的一点，F在p点可微分，那么在这一点的导数由JF(p)给出(这是求该点导数最简便的方法)。在此情况下，由F(p)描述的线性算子即接近点p的F的{zy}线性逼近，x逼近与p

}-

] 例子

由到直角坐标系的转化由F函数给出:R × [0,π] × [0,2π] → R3

此坐标变换的雅可比矩阵是

R4的f函数:

其雅可比矩阵为:

此例子说明雅可比矩阵不一定为方矩阵。

] 在动态系统中

考虑形为x' = F(x)的，F : Rn → Rn。如果F(x0) = 0，那么x0是一个驻点。系统接近驻点时的表现通常可以从JF(x0)的来决定。

] 雅可比行列式

如果m = n，那么F是从n维空间到n维空间的函数，且它的雅可比矩阵是一个。于是我们可以取它的行列式，称为雅可比行列式。

在某个给定点的雅可比行列式提供了F在接近该点时的表现的重要信息。例如，如果F在p点的雅可比行列式不是零，那么它在该点具有。这称为。更进一步，如果p点的雅可比行列式是，则F在p点的取向不变；如果是负数，则F的取向相反。而从雅可比行列式的，就可以知道函数F在p点的缩放因子；这就是为什么它出现在中。

例子

设有函数F : R3 → R3，其分量为：

则它的雅可比行列式为：

从中我们可以看到，当x1和x2同号时，F的取向相反；该函数处处具有反函数，除了在x1 = 0和x2 = 0时以外